Multiplier des nombres au delà des capacités d'Excel

3eme article pour ce sujet.

Après GMAX/GMIN, GSOMME, voilà GPRODUIT.

Précédents articles :
>MIN/MAX Dépasser la limite de précision des 15 chiffres
>Additions et soustractions au delà du mur des Billions

Toujours avec une fonction LAMBDA pour dépasser cette limite

Je vous proposer de créer une fonction LAMBDA dont l'objectif est de multiplier 2 valeurs dépassant les 15 chiffres ou/et dont le résultat dépasse les 15 chiffres significatif.

Cahier de charges :

• Valeurs pouvant être en numériques (limité par Excel à 15 chiffres) ou alphanumériques (texte).
• Valeurs pouvant être constituées de centaines de chiffres.
• Valeurs pouvant être positives ou négatives.
• Valeurs pouvant avoir une partie décimale ou non.

Principe général de la fonction

1. On passe en nombre entier positif en "effaçant" la virgule et le signe moins.
2. On utilise l'algorithme d'Anatoli Karatsuba (voir https://fr.wikipedia.org/wiki/Algorithme_de_Karatsuba ) de manière récursive afin de "descendre" à une taille de multiplicateur/multiplicande suffisante pour un résultat compatible avec Excel (<15 chiffres) =>algorithme de type "Diviser pour régner".
3. On replace la virgule et le signe moins si nécessaire.

Les principales difficultés :

• Mettre en place la récursivité de la fonction LAMBDA.
• Repositionner la virgule et le signe moins si nécessaire.
• Supprimer les 0 superflus.

Comparaison des algorithmes classique et Karatsuba

L'algorithme classique (division Euclidienne)

Celui appris à l'école.

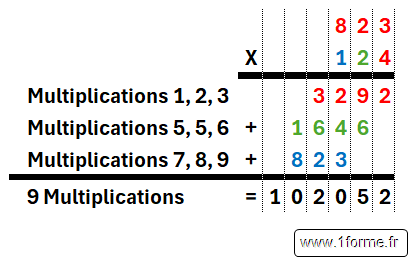
L'algorithme Karatsuba

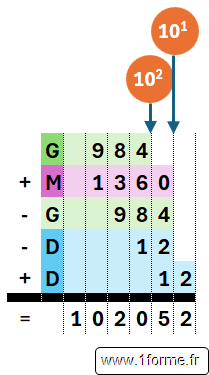
On ne fait que 3 sous-multiplications (intérêt en terme de vitesse de traitement) qui ne portent que sur des portions des multiplicateur/multiplicande (ce qui nous intéresse ici).

Création des fonctions préliminaires

Nous allons avoir besoin des fonctions suivantes.

Fonctions déjà créées dans les articles précédents

Voir l'article MIN/MAX Dépasser la limite de précision des 15 chiffres

• _NET : Fonction permettant de nettoyer les chaines des caractères indésirables, supprimer les séparateurs de milliers (ceci pouvant fausser les résultats).
• _SEP : Fonction permettant de répartir les chiffres de la partie entière d'un nombre en groupe de 3 (séparateur de milliers).
• _UNIF.DEC : Fonction permettant d'uniformiser le nombre de décimales.
• GSOMME : Fonction permettant de faire des additions en dépassant la limite de 15 chiffres significatifs.

La fonction _GPRODUIT

Rôle

• Faire le produit de 2 valeurs entières positives fournies par la fonction GPRODUIT (voir définition plus bas).

Principe

• On va suivre l'algorithme de Karatsuba dont le principe est de diviser chaque chaîne de chiffres en deux "sous- chaînes" pour obtenir le résultat par des multiplications (Exemple : La multiplication de 2 nombres de 4 chiffres chacun se fera en plusieurs multiplications de nombre de 2 chiffres).
• Par un traitement récursif, chacune de ces multiplications portant sur des chaines plus courtes peuvent elle aussi être faite en appliquant l'algorithme de Karatsuba et ainsi de suite (récursivité).
• Pour s'assure d'arriver à une taille suffisamment petite (<8 chiffres pour un résultat à <15 chiffres), on va faire en sorte que les deux valeurs de départ aient le même nombre de caractères.
  
  Illustration du problème généré par le cas de valeurs ayant un nombres de caractères trop différent :
  >Valeur 1 : "111 222 333 444 555 666 600 500 400 300 200 100" (36 caractères).
  >Valeur 2 : "46" (2 caractères).
  • 1ère appel :
    • "111 222 333 444 555 666 600 500 400 300 200 100" est divisé en "111 222 333 444 555 666" et "600 500 400 300 200 100".
    • "46" est divisé en "4" et "6".
  • 2ème appel :
    • On pourrait continuer de diviser "111 222 333 444 555 666" et "600 500 400 300 200 100",
    • mais "4" et "6" ne sont plus divisible et les chaînes "111 222 333 444 555 666" et "600 500 400 300 200 100" sont toujours trop longues pour être exploitées par Excel (18 caractères) !
• On arrête ces appels récursifs quand la longueur d'une des deux chaînes devient compatible avec les capacités d'Excel et on réalise alors la multiplication normalement.

Syntaxe

=LAMBDA(V_1;V_2;LET(
  nbCV1;  NBCAR(V_1);
  nbCV2;  NBCAR(V_2);
  Cp;     ABS(nbCV1-nbCV2);
  mxNbC;  MAX(nbCV1;nbCV2);
  V_1Cp;  V_1 &REPT("0";mxNbC-nbCV1);
  V_2Cp;  V_2 &REPT("0";mxNbC-nbCV2);
  mi;     ARRONDI.INF(mxNbC/2;0);
  SI(mi<4;(V_1Cp*V_2Cp/10^Cp); LET(
    DVal1;  GAUCHE(V_1Cp;mxNbC-mi);
    FVal1;  DROITE(V_1Cp;mi);
    DVal2;  GAUCHE(V_2Cp;mxNbC-mi);
    FVal2;  DROITE(V_2Cp;mi);
    D;      _GPRODUIT(FVal1;FVal2);
    M;      _GPRODUIT(_GSOMME(DVal1;FVal1);_GSOMME(DVal2;FVal2));
    G;      _GPRODUIT(DVal1;DVal2);
    res;    GSOMME(G&REPT("0";mi*2);GSOMME(GSOMME(ASSEMB.H(M;"-"&G;"-"&D);;)&REPT("0";mi);D;););
  STXT(res;1;NBCAR(res)-Cp)
))
))

Arguments

• V_1 : 1ere valeur à multiplier (obligatoire).
• V_2 : 2ème valeur à multiplier (obligatoire).

Variables

• nbCV1 : Nombre des caractères de la chaîne.
• nbCV1 : Nombre des caractères de la chaîne.
• Cp : Nombre de 0 à ajouter pour égaliser les chaînes (l'uniformisation des chaînes est à faire à chaque appel de la fonction).
  • Illustration du problème :
    • Exemple où les chaînes devaient être à 4 caractères pour cette itération mais l'itération précédente a "simplifié" V_2 et a renvoyé "5" au lieu de "0005", bloquant ainsi les itérations suivantes.
    • De plus, "0005" ne serait pas bon non plus pour la prochaine itération ("00" et "05").
    • "5" sera donc remplacer par "5000".
• mxNbc : Nombre de caractères de la plus grande chaîne.
• V_1Cp : Valeur V_1 complétée avec des 0 si nécessaire.
  • Par exemple si V_1 ="5" et V_2="1234", V_1 devient "5000".
• V_2Cp : Valeur V_1 complétée avec des 0 si nécessaire.
• mi : Milieu de la chaîne servant de point de césure.
• DVal1: Début de la chaine V_1Cp.
• FVal1 : Fin de la chaine V_1Cp.
• DVal2 : Début de la chaine V_2Cp.
• FVal2 : Fin de la chaine V_2Cp.
• D : Calcul partie Droite.
• M : Calcul partie Milieu (utilisation de la fonction _GSOMME au lieu de GSOMME par soucis d'optimisation).
• G : Calcul partie Gauche.
• res : Résultat brute ayant des 0 en trop (les 0 complémentaires ajoutés) et calculé selon la formule : G*10^mi*2 + (M-G-D)*10^mi + D.
  (Utilisation de la fonction GSOMME au lieu de _GSOMME par précaution bien que je pense inutile)

Retour

• Soit on multiplie V_1Cp et V_2Cp car ils sont compatibles avec un calcul standard (mi<4, soit 2 chaînes de 6 caractères, soit un résultat a 12 chiffres).
• Soit on utilise le résultat de l'itération suivante res.
• Dans les 2 cas, on supprime les 0 complémentaires ajoutés.

Création de la fonction GPRODUIT

Rôle

• Traiter les valeurs de départ pour les rendre compatibles avec la fonction _GPRODUIT.
• Traiter le résultat de la fonction _GDIV pour obtenir le résultat final.

Principe

• On mémorise le signe du résultat.
• On passe toutes les valeurs en entiers positifs constitués du même nombre de chiffres (mémorisation de la puissance de 10 appliquée).
• On réalise le produit avec la fonction _GPRODUIT.
• On efface les 0 superflus (à droite) dans la partie décimale.
• On ajoute le signe, les séparateurs de Milliers et la virgule si nécessaire.

Syntaxe

=LAMBDA(Valeur1;Valeur2;Separateur;LET(
   VN;       OUX(GAUCHE(Valeur1;1)="-";GAUCHE(Valeur2;1)="-");
   mVNet;    SUBSTITUE(_NET(ASSEMB.V(Valeur1;Valeur2));"-";"");
   mVUnif;   _UNIF.DEC(mVNet);
   mVUc1;    index(mVUnif;0;1);
   posVirg;  SOMME(SIERREUR(NBCAR(mVUc1)-CHERCHE(",";mVUc1);0));
   mVComp;   SUBSTITUE(mVUc1;",";"");
   res;      SI(OU(SUBSTITUE(INDEX(mVNet;{1;2};1);"0";"")="");0;_GPRODUIT(INDEX(mVComp;1;1);INDEX(mVComp;2;1)));
   nbCR;     NBCAR(res);
   resPE;    SI(posVirg>=nbCR;0;STXT(res;1;nbCR-posVirg));
   resPD;    DROITE(REPT("0";posVirg)&res;posVirg);
   resPDN;   SIERREUR(REDUCE(
                             "";
                             STXT(resPD;SEQUENCE(NBCAR(resPD);;NBCAR(resPD);-1);1);
                             LAMBDA(c;v;SI((c="")*(v="0");"";v)&c));"");
   SI(VN*(res<>"0");"-";"")
     &SI(Separateur;_SEP(resPE);resPE)
     &SI(resPDN="";"";","&resPDN)
   ))

Arguments

• Valeur1 : 1ere valeur à multiplier (obligatoire).
• Valeur2 : 2eme valeur à multiplier (obligatoire).
• Separateur : Booléen, indiquant si le résultat doit utiliser des séparateurs de Milliers pour la partie entière (obligatoire).

Variables

• VN : Booléen indiquant si le résultat est une Valeur Négative.
• mVNet : Matrice des Valeurs Nettoyées et passées en valeur absolue (sans signe).
• mVUnif : Matrice des Valeurs avec un même nombre de décimales (ajout de 0 complémentaires) et nombre de 0 en complément.
• mVUc1 : Matrice des Valeurs sans la colonne indiquant le nombre de 0 en complément.
• posVirg : Position de la Virgule pour la repositionner en fin de traitement.
• mVComp : Matrice des Valeurs sans virgule.
• res: Résultat du produit des 2 valeurs entières de mVComp.
  • Si une des 2 valeurs est à 0 on renvoie 0.
• nbCR : Nombre de Caractères du Résultat.
• resPE : Partie Entière du Résultat avec gestion du cas ou le résultat est entre 1 et -1 (ex : 0.00015 ou -0.0024).
• resPD : Partie Décimale du Résultat avec gestion du cas ou le résultat est entre 1 et -1 (ex : 0.00015 ou -0.0024).
• resPDN : Partie Décimale Nettoyée des 0 en trop (à droite du dernier chiffre significatif).

Retour

On ajoute :

• Le signe - (moins) si nécessaire,
• la Partie Entière avec des séparateurs de Millier si nécessaire,
• la virgule et la Partie Décimale si nécessaire.

Exemple

• Valeur 1 : 3141592653589793238462643383279502884197169399375105820974944592 (64 chiffres).
• Valeur 2 : 2718281828459045235360287471352662497757247093699959574966967627 (64 chiffres).
• Résultat : 8 539 734 222 673 567 065 463 550 869 546 574 495 034 888 535 765 114 961 879 601 127 067 743 044 893 204 848 617 875 072 216 249 073 013 374 895 871 952 806 582 723 184 (127 chiffres).

Merci pour votre attention bienveillante.