Additions et soustractions au delà du mur des Billions

Illustration

2ème article sur ce thème.

Voir article précédent : MIN/MAX Dépasser la limite de précision des 15 chiffres.

Rappel problématique

Il existe une limite au nombre de chiffres significatifs utilisable par Excel :

• Si l'on saisit un nombre de plus de 15 chiffres, Excel enregistrera la saisie comme une chaîne de texte (gênant pour faire des calculs).
• Si l'on génère une formule renvoyant un résultat de plus de 15 chiffres, les chiffes après le 15eme (les moins significatifs) seront remplacés par des 0.

Une LAMBDA pour dépasser cette limite

Je vous proposer de créer une fonction LAMBDA dont l'objectif est d'additionner 2 valeurs ou plus.

Cahier de charges :

• Valeurs pouvant être en numériques (limité par Excel à 15 chiffres) ou alphanumériques (texte).
• Valeurs pouvant être constituées de centaines de chiffres.
• Valeurs pouvant être positives ou négatives (équivalant à une soustraction dans ce cas).
• Valeurs pouvant avoir une partie décimale ou non.
• Valeurs pouvant être contenues dans 1 ou 2 plages de dimensions et d'orientations libres.

Créer cette formule pour des valeurs uniquement positives ou uniquement négatives est "assez facile" mais mixer les deux types est un autre défi !

La formule est proposée en l'état. Je ne garantit pas la justesse des résultats bien que je l'ai testée sur de nombreux exemples (l' "accouchement" a été assez douloureux 😁 donc difficile d'être vraiment sûr de soi !).

Principe général de la fonction

1. "Diviser pour régner" : On va additionner séparément les valeurs positives et négatives puis on s'occupera de la soustraction dans un second temps.
2. Pour les additions :
   1. On uniformise le nombre de décimales et on supprime la virgule et le signe - pour se retrouver dans le cas d'une addition de valeurs entières positives.
   2. On va encore diviser chaque nombre en plusieurs valeurs représentant chaque classe (Unités, Milliers, Millions, Milliards, Billions, Billiards...).
   3. Additionner chaque classe en prenant en compte les retenues.
   4. Réassembler la valeur finale à partir de ces "sous totaux".
3. Pour la soustraction :
   1. On va faire comme à l'école : On soustrait le plus grand du plus petit en prenant en compte les retenues et compléments en découlant.

Après de nombreuses tentatives, j'ai opté pour cette solution qui n'est peut-être pas la plus rapide mais me semble "simple".

Les principales difficultés :

• Prendre en compte les retenues impactant la classe/chiffre suivant(e).
• Générer les "valeurs complémentaires" générées pas les retenues de la soustraction.
• Repositionner la virgule si nécessaire.
• Supprimer les 0 superflus.

Création des fonctions préliminaires

Nous allons avoir besoin des fonctions suivantes.

Fonctions déjà créées

Voir l'article MIN/MAX Dépasser la limite de précision des 15 chiffres

• _NET : Fonction permettant de nettoyer les chaines des caractères indésirables, supprimer les séparateurs de milliers (ceci pouvant fausser les résultats).
• _UNIF.DEC : Fonction permettant d'uniformiser le nombre de décimales.
• _SEP : Fonction permettant de répartir les chiffres de la partie entière d'un nombre en groupe de 3 (séparateur de milliers).
• GMAX : Fonction renvoyant la plus grande valeur d'une liste de valeurs. Ces valeurs pouvant être constituées de plus de 15 chiffes.

La fonction _GSOMME

Rôle

Faire la somme de valeurs entières positives fournies par la fonction GSOMME (voir plus bas).

Principe

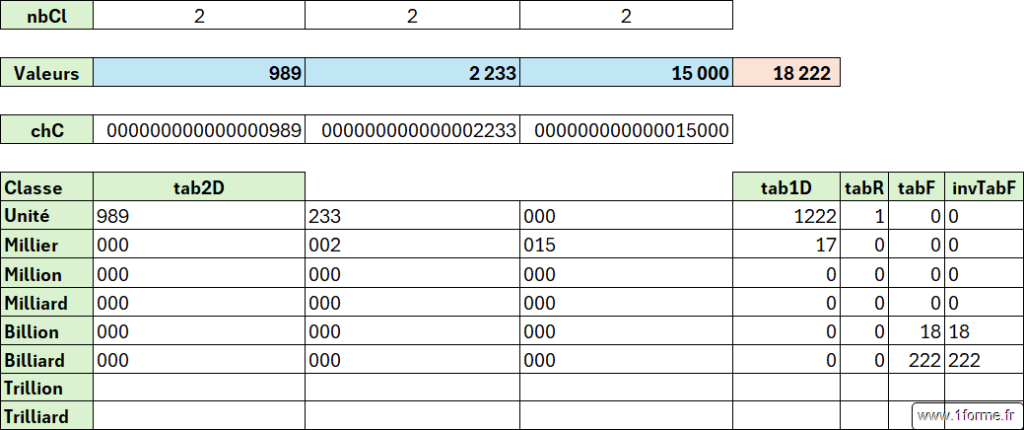
• On décompose les valeurs en classe.
• On additionne toutes les valeurs de même classe.
• On calcule les retenues à appliquer.
• On réassemble les classes en ajoutant les retenues.

Syntaxe

=LAMBDA(Plage1;Plage2;LET( 
  PlageC; ASSEMB.H(DANSLIGNE(SIERREUR(Plage1;0);3);
                   DANSLIGNE(SI(ISOMITTED(Plage2);0;SIERREUR(Plage2;0));3));
  nbCl;   PLAFOND.MATH(MAX(NBCAR(PlageC));3)/3+4;
  chC;    REPT(0;nbCl*3-NBCAR(PlageC))&PlageC;s;SEQUENCE(nbCl;;nbCl;-1);
  tab2D;  STXT(chC;3*s-2;3);
  tab1D;  BYROW(tab2D;LAMBDA(v;SOMME(v*1)));
  tabR;   SCAN(0;tab1D;LAMBDA(c;v;c-c+ENT((v+c)/1000))); 
  tabF;   DROITE(MAP(s;LAMBDA(i;INDEX(tab1D;i)+SI(i=1;0;INDEX(tabR;i-1))));3)*1; 
  res;    REDUCE("";tabF;LAMBDA(c;v;c&SI(ET(v=0;c="");"";SI(c="";v;TEXTE(v;"000")))));
  SI(res="";0;res)
))

Arguments

• Plage1 : Valeur ou plage/matrice de valeurs à additionner (obligatoire).
• Plage2 : Valeur ou plage/matrice de valeurs à additionner (facultatif).

Variables

• PlageC : Matrice des données des 2 plages passées en une ligne (on suppose qu'il n'y a pas de séparateurs de Millier=> supprimés en pré-traitement).
• nbCl : Calcul du nombre de Classes. On en ajoute 4 pour être en mesure d'absorber les 17 milliards de retenues théoriquement possibles.
• chC : Matrice des valeurs Complétés où l'on a ajouté des 0 à gauche pour uniformiser le nombre de caractères des nombres pour le futur découpage en classes.
• tab2D : Matrice résultant du découpage en classes.
• tab1D : Matrice de la somme des classes de tab2D.
• tabR : Matrice des retenues à appliquer (utilisation insolite de SCAN où l'on utilise le cumul pour ne récupérer que la valeur précédente d'où le c-c !).
• tabF : Matrice Finale (valeurs tab1D + tabR décalée de 1) inversant l'ordre des valeurs en prévision de la concaténation futur.
• res : Résultat final via la concaténation des classes de tabF.

Retour

• On gère le cas où le résultat est 0.

La fonction GSOMME

Rôle

Faire la somme de valeurs décimales.

Principe

• On passe toutes les valeurs en entiers.
• On ajoute toutes les valeurs de même signe ensemble.
• On calcule les retenues à appliquer.
• On réalise la soustraction chiffre par chiffre en prenant an compte les retenues et compléments à appliquer.
• On réassemble les chiffres, virgule et signe.

=LAMBDA(Plage1;Plage2;Separateur;LET(
  mVComp;   INDEX(_UNIF.DEC(_NET(ASSEMB.V(DANSCOL(Plage1;3);
                                          DANSCOL(SI(ISOMITTED(Plage2);0;Plage2);3))));0;1);
  mVal1;    INDEX(mVComp;1);
  nbDec;    SIERREUR(NBCAR(mVal1)-CHERCHE(",";mVal1);0);
  mV;       SUBSTITUE(mVComp;",";"");
  mVP;      FILTRE(mV;(GAUCHE(mV;1)<>"-"));
  mVN;      SUBSTITUE(FILTRE(mV;GAUCHE(mV;1)="-");"-";"");
  tVP;      _GSOMME(mVP;);
  tVN;      _GSOMME(mVN;);
  tVLi1;    GMAX(ASSEMB.V(tVP;tVN);VRAI;FAUX);
  tVLi2;    SI(tVLi1=tVP;tVN;tVP);
  nbCLi1;   NBCAR(tVLi1);
  nbCLi2;   NBCAR(tVLi2);
  mCLi1;    STXT(tVLi1;SEQUENCE(;nbCLi1;1;1);1);
  mCLi2;    STXT(tVLi2;SEQUENCE(;nbCLi2;1;1);1);
  mCLi2Comp;SI(nbCLi1<>nbCLi2;ASSEMB.H(SEQUENCE(;nbCLi1-nbCLi2;0;0);mCLi2);mCLi2);
  s;        SEQUENCE(;nbCLi1;nbCLi1;-1);
  mR;       SCAN(0;s;LAMBDA(c;v;c-c+((INDEX(mCLi1;1;v)-c)<INDEX(mCLi2Comp;1;v)*1)));
  mRS;      INDEX(mCLi1;1;nbCLi1-s+1)+INDEX(mR;1;s)*10
                -SI(s>1;INDEX(mR;1;s-1);0)-INDEX(mCLi2Comp;1;nbCLi1-s+1);
  rF;      SI(tVN=0;tVP;SI(tVP=0;tVN;REDUCE("";mRS;LAMBDA(c;v;SI((c="")*(v=0);"";c&v)))));
  rFPE;    STXT(rF;1;NBCAR(rF)-nbDec);
  SI(tVLi1=tVN;"-";"")
    &SI(NBCAR(rFPE)=0;"0";SI(OU(ISOMITTED(Separateur);1-Separateur);rFPE;_SEP(rFPE)))
    &SI(nbDec;","&DROITE(rF;nbDec);"")
))

Arguments

• Plage1 : Valeur ou plage/matrice de valeurs à additionner (obligatoire).
• Plage2 : Valeur ou plage/matrice de valeurs à additionner (facultatif).
• Separateur : Booléen, indiquant si le résultat doit afficher des séparateurs de milliers (obligatoire).

Variables

• mVComp : Matrice des données des 2 plages passées en une colonne, nettoyées et avec uniformisation du nombre de décimales (on ne garde que la colonne des valeurs, pas celle de 0 ajoutés).
• mVal1 : 1ere valeur afin d'en déduire le nombre de décimales dans nbDec.
• nbDec : Nombre de décimales, utilisé pour replacer la virgule en fin de traitement.
• mV : Matrice des valeurs sans le caractère virgule (on passe donc en "entier").
• mVP : Matrice des valeurs Positives et nulles.
• mVN : Matrice des valeurs Négatives sans signe (valeur absolue).
• tVP : Total des valeurs Positives.
• tVN : Total des valeurs Négatives.
• mVal : Matrice des 2 valeurs à soustraire.
• tVLi1 : Le total le plus grand entre tVP et tVN (pour soustraire le plus petit du plus grand).
• tVLi2 : Le total le plus petit entre tVP et tVN (pour soustraire le plus petit du plus grand).
• nbCLi1 : Nombre de caractères de la ligne 1 (Ligne correspondante au plus grand).
• nbCLi2 : Nombre de caractères de la ligne 2 (Ligne correspondante au plus petit).
• mCLi1 : Matrice des caractères/chiffres de tVLi1.
• mCLi2 : Matrice des caractères/chiffres de tVLi2.
• mCLi2Comp : Matrice des caractères/chiffres de tVLi2 complétée de 0 à gauche pour avoir la même taille que celle de la ligne1.
• s : Séquence de chiffres à rebours servant d'indice pour parcourir les matrices/chaînes de droite à gauche..
• mR : Matrice des retenues qui devront être appliquées (utilisation insolite de SCAN où l'on utilise le cumul pour ne récupérer que la valeur précédente d'où l'étrange c-c !).
• mRS : Matrice Résultat de la Soustraction avec prise en compte des retenues et compléments à 10.
• rF : Résultat final :
  • Soit tVP si que des valeurs positives,
  • Soit tVN si que des valeurs négatives,
  • Soit mRS si des valeurs positives et négatives avec suppression des 0 ajoutés à gauche (cf mCLi2Comp).
• rFPE : Extraction de la partie entière (pour positionner la virgule et mettre en place les séparateurs de Millier si nécessaire).

Retour

On ajoute :

• Le signe - (moins) si nécessaire,
• un 0 si la partie entière est vide,
• la partie entière avec les séparateurs de Millier si nécessaire,
• la virgule et la partie décimale si nécessaire.

Tests réalisés

• Addition de 50 000 paires de nombres de 13 chiffres.
• Soustraction de 50 000 paires de nombres de 13 chiffres.
• Addition d'une plage de 3 000 valeurs 998 001 renvoyant 2 994 003 000 comme résultat. Les classes Milliards (2) et Millions (994) sont générées par le cumul des retenues !
• Additions et soustractions de deux nombres de 200 chiffres chacun.
• Divers autres tests.

Je ne me suis pas penché sur les limites et temps de calcul de cette fonction.

À suivre les fonctions GPRODUIT, GMOYENNE, GECARTYPE, GGRANDE.VALEUR...😁

Merci pour votre attention bienveillante.