La division au delà de la limite des 15 chiffres significatifs

4eme article pour ce sujet.

Après GMAX/GMIN, GSOMME, GPRODUIT, on arrive à GDIV.

Précédents articles :
>MIN/MAX Dépasser la limite de précision des 15 chiffres
>Additions et soustractions au delà du mur des Billions
>

Toujours avec une fonction LAMBDA pour dépasser cette limite

Je vous proposer de créer une fonction LAMBDA dont l'objectif est de diviser 2 valeurs dépassant les 15 chiffres ou/et dont le résultat dépasse les 15 chiffres significatifs.

Cahier de charges :

• Valeurs pouvant être en numériques (limité par Excel à 15 chiffres) ou alphanumériques (texte).
• Valeurs pouvant être constituées de centaines de chiffres.
• Valeurs pouvant être positives ou négatives.
• Valeurs pouvant avoir une partie décimale ou non.

Principe général de la fonction

1. On passe en nombre entier positif en "effaçant" la virgule et le signe moins.
2. On utilise une méthode basée sur la division de Joseph Fourrier (voir Fourier division - Wikipedia) de manière récursive afin de calculer terme B.
3. On replace la virgule et le signe moins si nécessaire.

Méthode de Fourier

Pour diviser C par A, on décompose le dividende en terme C₁, C₂... et le diviseur en A₁, A₂...

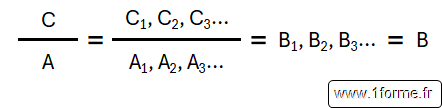
On calcule B₁

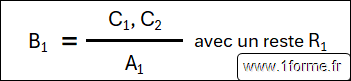
On calcule B₂

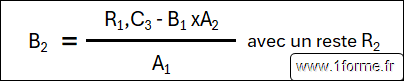
On calcule B₃

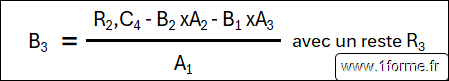
On réassocie les termes B : B₁, B₂, B₃...

Les principales difficultés

• Mettre en place la récursivité de la fonction LAMBDA.
• Repositionner la virgule et le signe moins si nécessaire.

Création des fonctions préliminaires

Nous allons avoir besoin des fonctions suivantes.

Fonctions déjà créées dans les articles précédents

Voir l'article MIN/MAX Dépasser la limite de précision des 15 chiffres

• _NET : Fonction permettant de nettoyer les chaines des caractères indésirables, supprimer les séparateurs de milliers (ceci pouvant fausser les résultats).
• _SEP : Fonction permettant de répartir les chiffres de la partie entière d'un nombre en groupe de 3 (séparateur de milliers).
• _UNIF.DEC : Fonction permettant d'uniformiser le nombre de décimales.
• GSOMME : Fonction permettant de faire des additions en dépassant la limite de 15 chiffres significatifs.
• GPRODUIT : Fonction permettant de faire des multiplications en dépassant la limite de 15 chiffres significatifs.

La fonction GENT

Rôle

• Renvoyer la partie entière d'une valeur pouvant dépasser les 15 chiffres significatifs.

Principe

• On va extraire la partie à gauche de la virgule en l'augmentant de 1 pour les valeurs négatives.

Syntaxe

=LAMBDA(Valeur;LET(
   n; NBCAR(Valeur);
   p; CHERCHE(",";Valeur);
   GSOMME(GAUCHE(Valeur;SIERREUR(p-1;n)); -(GAUCHE(Valeur;1)="-")*SIERREUR((STXT(Valeur;p+1;n)*1)<>0;0);)
 ))

Arguments

• Valeur : Valeur à utiliser.

Variables

• n : Nombre de caractère de la valeur.
• p : Position de la virgule.

Retour

• On renvoie :
  • La valeur s'il n'y a pas de décimales.
  • Les chiffres à gauche de la virgule (24,8 => 24) pour les valeurs positives.
  • Les chiffres à gauche de la virgule "augmentés" de 1 (-24,8 => -25) pour les valeurs négatives suivant ainsi la logique de la fonction ENT originale.

La fonction _GDIV

Rôle

• Générer la matrice des divisions croisées (valeurs B) à partir de 2 valeurs entières positives fournies par la fonction GDIV (voir plus bas).

Principe

• On va suivre l'algorithme de Joseph Fourrier dont le principe est de diviser chaque chaîne en des paires de chiffres que l'on va diviser.

Syntaxe

=LAMBDA(mValC;mValA;nbB;DivA1;
 SI(nbB=1;
    LET(
        DivD;SIERREUR(INDEX(mValC;nbB);"00")&SIERREUR(INDEX(mValC;nbB+1);"00");
        ValB;GENT(DivD/DivA1);
        ValR;DivD-DivA1*ValB;
        ASSEMB.V(ValR;ValB)
       );
    LET(
        mR;_GDIV(mValC;mValA;nbB-1;DivA1);
        mB;EXCLURE(mR;1);
        mA;PRENDRE(EXCLURE(mValA;1);nbB-1);
        DivD;(INDEX(mR;1)&SIERREUR(INDEX(mValC;nbB+1);"00"))-
              GSOMME(map(sequence(nbval(mB));LAMBDA(v;GPRODUIT(index(mB;v;1);index(mA;v;1);))) ;;);
	      ValB;GENT(DivD/DivA1);
        ValR;GSOMME(DivD-GPRODUIT(DivA1;ValB;);;);
        ASSEMB.V(ValR;ValB;EXCLURE(mR;1))
       ) ) )

Arguments

• mValC : Dividende (obligatoire).
• mValA : Diviseur (obligatoire).
• nbB : Nombre de récursions générant les termes B.
• DivA1 : Premier terme A (A₁) identique pour chaque récursion.

Variables

• 1^er LET (dernière itération).
  • DivD : Génération du dividende (ici "C₁, C₂").
    • Le SIERREUR permet de continuer les itérations au-delà du nombre de paires des valeurs de départ.
  • ValB : Valeur B₁.
  • ValR : 1er reste (R₁).
• 2^eme LET.
  • mR : Génération de la récursivité (arrêté via nbB-1).
  • DivD : Génération du dividende.
    • "R_n-1, C_n+1" - Σ( B_{[n-1 à 1]} * A_{[2 à n]} ).
    • Le SIERREUR permet de continuer les itérations au-delà du nombre de paires des valeurs de départ.
  • ValB : Valeur B_n .
    • La division ici est problématique dépassant parfois la limite des 15 chiffres significatifs.
    • Rappeler _GDIV ici ne semble pas pertinent en termes de puissance de calcul.
  • ValR : Reste (R_n).

Retour

• 1^er LET : On renvoie la matrice { R₁ ; B₁ }.
• 2^eme LET : On renvoie la matrice { R_n ; B₁ ; B₂...B_n }.

Création de la fonction GDIV

Rôle

• Traiter les valeurs de départ pour les rendre compatibles avec la fonction _GDIV.
• Traiter le résultat de la fonction _GDIV pour obtenir le résultat final.

Principe

• On mémorise le signe du résultat.
• On passe toutes les valeurs en entiers positifs constitués du même nombre de chiffres.
• On génère les paires et on calcule les termes B.
• On associe les termes B et on ajoute la virgule et le signe - si nécessaire.

Syntaxe

=LAMBDA(Valeur1;Valeur2;Decimales;Separateur;LET(
  Deci;    ABS(Decimales);
  Deci2;   Deci+2;
  VN;      OUX(GAUCHE(Valeur1;1)="-";GAUCHE(Valeur2;1)="-");
  mVNet;   INDEX(_UNIF.DEC(SUBSTITUE(_NET(ASSEMB.V(Valeur1;Valeur2));"-";""));;0;1);
  mVComp;  SUBSTITUE(mVNet;",";"");
  mNbCV;   NBCAR(mVComp);
  mxNbCV;  PAIR(MAX(mNbCV));
  V_1;     INDEX(mVComp;1;1)&REPT("0";mxNbCV-INDEX(mNbCV;1;1));
  V_2;     INDEX(mVComp;2;1)&REPT("0";mxNbCV-INDEX(mNbCV;2;1));
  mValC;   ETENDRE(STXT(V_1;SEQUENCE(NBCAR(V_1)/2;;1;2);2);mxNbCV+Deci2*2;;"00");
  mValA;   ETENDRE(STXT(V_2;SEQUENCE(NBCAR(V_2)/2;;1;2);2);mxNbCV+Deci2*2;;"00");
  mValB;   _GDIV(mValC;mValA;mxNbCV+Deci2*2;INDEX(mValA;1;1));
  res;     GSOMME(MAP(SEQUENCE(NBVAL(mValB));LAMBDA(v;INDEX(mValB;v;1)&REPT("00";v-1)));;);
  posV;    INDEX(mNbCV;1;1)-INDEX(mNbCV;2;1)
               + SI(INDEX(mNbCV;1;1)>=INDEX(mNbCV;2;1);
                    (GAUCHE(INDEX(mVComp;1;1);NBCAR(INDEX(mVComp;2;1)))>=INDEX(mVComp;2;1));
                    -(GAUCHE(INDEX(mVComp;2;1);NBCAR(INDEX(mVComp;1;1)))>=INDEX(mVComp;1;1)));
  resPE;   SI(posV<=0;0;GAUCHE(res;posV));
  resPD;   SI(posV<0;
              GAUCHE(REPT("0";-posV-1)&res;Deci);
              STXT(res&REPT("0";Deci);posV+1;Deci));
  SI(VN*((resPE<>0)+(resPD<>REPT("0";Deci)));"-";"")
    & SI(Separateur;_SEP(resPE);resPE)
    & SI(Deci=0;"";","&resPD)
))

Arguments

• Valeur1 : Dividende (obligatoire).
• Valeur2 : Diviseur (obligatoire).
• Decimales : Nombre de décimales du résultat (la dernière décimale du résultat ne sera pas arrondi).
• Separateur : Booléen, indiquant si le résultat doit utiliser des séparateurs de Milliers pour la partie entière (obligatoire).

Variables

• Deci : Nombre de décimales.
• Deci2 : Afin d'obtenir une précision correcte on va doubler le nombre. Le +2 est pour le cas ou Decimales est à 0 (2*0 c'est toujours 0).
• VN : Booléen indiquant si le résultat est une Valeur Négative.
• mVNet : Matrice des valeurs nettoyés, avec un même nombre de décimales (ajout de 0 complémentaires), sans signe.
• mVComp : Matrice des valeurs sans le caractère virgule (on se retrouve avec des entiers).
• mNbCV : Matrice du nombre de caractères des valeurs.
• mxNbCV : Nombre de caractère le plus grand arrondi à la valeur pair supérieure (Nécessaire pour découper les valeurs en paires complètes de chiffres.
• V_1 : Diviseur complété de 0 si nécessaire afin d'être de la même "taille" que le dividende.
• V_2 : Dividende complété de 0 si nécessaire afin d'être de la même "taille" que le diviseur.
• mValC : Matrice des paires de valeurs C_n (dimensionnée afin d'avoir une précision suffisante).
• mValA : Matrice des paires de valeurs A_n (dimensionnée afin d'avoir une précision suffisante).
• mValB : Matrice des valeurs B renvoyées par la fonction _GDIV (on double Deci2 afin d'obtenir une précision suffisante).
• res : Résultat brute après agrégation des valeurs B en décalant chaque valeurs de 2 rangs.
• posV : Détermination de la position de la virgule.
  • On décompte déjà l'écart entre le nombre de chiffres du Dividende par rapport au dividende (peut être négatif).
  • On ajoute 1 quand le chiffre du quotient est > 1.

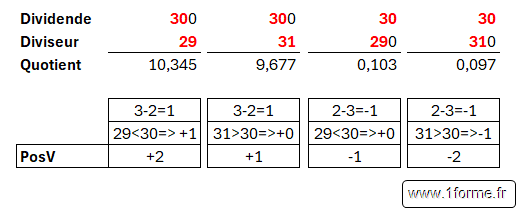
• resPE : Détermination de la partie Entière (Si le quotient est entre -1 et 1, on renvoie 0).
• resPD : Détermination de la partie Décimale (Si le quotient est entre -1 et 1, on complète avec des 0 à gauche du résultat sinon à droite du résultat en fonction de posV).
  Exemples :
  • posV=-2, res = 1234, on a :
    • resPE = 0
    • resPD = 01234
    • Soit finalement : 0,01234
  • posV=2, res = 1234, on a :
    • resPE = 12
    • resPD = 34
    • Soit finalement : 12,34

Retour

On ajoute :

• Le signe - (moins) si nécessaire (si une des 2 valeurs est négative et si le résultat n'est pas 0 ou 0,00...),
• la Partie Entière avec des séparateurs de Millier si nécessaire,
• la virgule et la Partie Décimale si nécessaire.

Limite d'utilisation

Cette fonction est beaucoup plus limitée que celles des précédents articles.

• La différence de chiffres entre Dividende et Diviseur semble être d'environ 40 chiffres.
• À partir de 120 chiffres (Dividende + Diviseur), le temps de calcul commence à être notable (1s de latence).
• Décimales limite vers 30 chiffres.

Merci pour votre attention bienveillante.