3 solutions pour une moyenne géométrique conditionnelle

Article à partir de la demande d'un utilisateur du forum.

Problème

L'utilisateur veut calculer la moyenne des notes en utilisant la moyenne géométrique et non arithmétique. Il désire décomposer les résultats par matière et par étudiant.

Les notes n'étant pas "dépendantes" les unes des autres, je ne comprends pas trop l'intérêt de ce choix mais n'étant pas mathématicien je vais éviter de faire preuve ultracrépidarianisme (ça en jette ! 😁).

Voir https://fr.wikipedia.org/wiki/Moyenne_g%C3%A9om%C3%A9trique

Excel met à notre disposition la fonction MOYENNE.ENS mais il s'agit ici de la moyenne arithmétique, il va donc falloir faire une formule dédiée.

Je vous propose 3 solutions (version du futur 😊, actuelle, ancienne)

Données de test

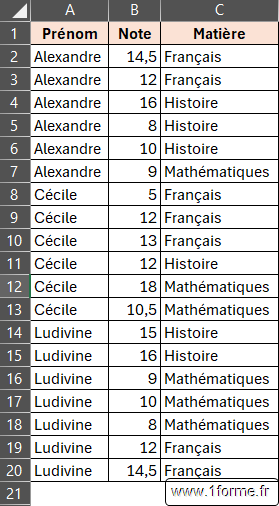
Principe du calcul

On va repartir de l'équation de base.

(Fonction MOYENNE.GEOMETRIQUE - Support Microsoft)

La racine sera générée en élevant à la puissance inverse.

Solution 1 : En une formule via la nouvelle fonction PIVOTER.PAR

Voir Les nouvelles fonctions GROUPER.PAR (GROUPEBY) et PIVOTER.PAR (PIVOTBY)

=PIVOTER.PAR(A2:A20 ; C2:C20 ; B2:B20 ; LAMBDA(v;PRODUIT(v)^(1/NB(v)));0;0;1;0;1)

• On utilise ici une fonction de calcule personnalisée (Rappel : le signe ^ est l'élévation à la puissance).

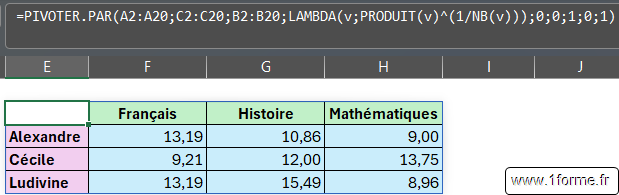
Solution 2 : En 3 formules

Formule 1 : Liste des étudiants

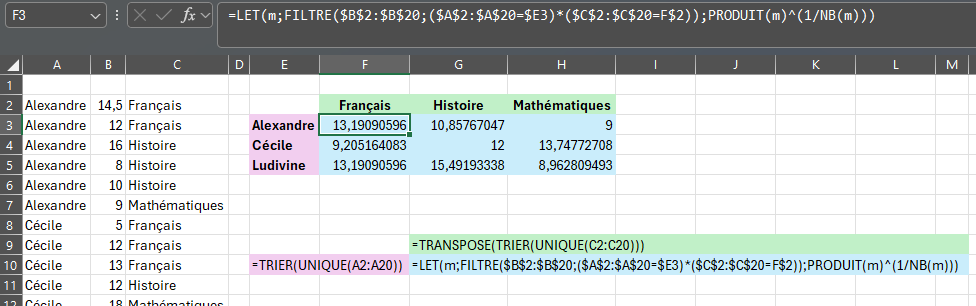
=TRIER(UNIQUE(A2:A20))

Formule 2 : Liste des matières

=TRANSPOSE(TRIER(UNIQUE(C2:C20)))

Formule 3 : La moyenne

Formule à recopier en ligne et colonne

=LET(m;FILTRE($B$2:$B$20;($A$2:$A$20=$E3)*($C$2:$C$20=F$2));PRODUIT(m)^(1/NB(m)))

• m : matrice des valeurs (note) correspondantes à la ligne (étudiant) et à la colonne (matière).

Solution 3 : Anciennes versions d'Excel

Formules matricielles donc à valider par CTRL+MAJ+ENTRER

Voir Excel et les matrices (pas celles du cours de mathématiques)

Formule 1 : Liste des étudiants

{=SIERREUR(
    INDEX(Pl_Prenom;
      PETITE.VALEUR(
         SI(FREQUENCE(
              SI(Pl_Prenom<>"";EQUIV(Pl_Prenom;Pl_Prenom;0));
              LIGNE(Pl_Prenom)-1);
            LIGNE(Pl_Prenom)-1);
      LIGNES(E$3:E3))
          );
    "")}

Mise en œuvre intéressante de la fonction FREQUENCE et PETITE.VALEURS dans ce cas.

• Pl_Prenom : Plage des prénoms ($A$2:$A$20).
• => On cherche la position de la 1^ere occurrence de chaque prénom.
  • SI(Pl_Prenom<>"";EQUIV(Pl_Prenom;Pl_Prenom;0)) : Matrice représentant la position de la 1^ere occurrence de chaque prénom.
    • Ici {1;1;1;1;1;1;7;7,... 13} => sera utilisée comme la matrice des données dans la fonction FREQUENCE.
• => On va maintenant chercher à éliminer les répétitions de n° de lignes dans la matrice.
  • LIGNE(Pl_Prenom)-1) : Matrice constituée d'une séquence de valeurs.
    Ici {1;2;3,... 19} => sera utilisée comme la matrice des classes pour la fonction FREQUENCE.
  • La fonction FREQUENCE renvoie la matrice suivante {6;0;0;0;0;0;6;0;0;0;0;0;7;0;0;0;0;0;0}
    • On a perdu les numéros de lignes mais on sait que les valeurs à "ignorées" sont celles à 0.
• => On va maintenant chercher à rétablir les n° de lignes correspondantes aux plus petites valeurs de la matrice précédente mais seulement celle différentes de 0 afin de les "extraire" avec la fonction PETITE.VALEUR.
  • Il faudra donc remplacer les 0 par une valeur qui ne sera non pris en compte par la fonction PETITE.VALEUR (valeur FAUX).
  • On va donc faire évaluer la formule : SI( {6;0;0;0;0;0;6;0;0;0;0;0;7;0;0;0;0;0;0} ; {1;2;3,... 19})
    • Les valeurs 0 seront considérées comme FAUX, par conséquent la fonction SI renverra la partie "Valeur_si_faux". Celle-ci n'étant pas précisée, on obtient la valeur logique FAUX.
    • Les valeurs différentes de 0 seront considérées comme VRAI, par conséquent la fonction SI renvoie la partie "Valeur_si_vrai" soit les n° de lignes.
    • On obtient la matrice {1;FAUX;FAUX;FAUX;FAUX;FAUX;7;FAUX;FAUX;FAUX;FAUX;FAUX;13;FAUX;FAUX;FAUX;FAUX;FAUX;FAUX}.
• => On va maintenant prendre la 1ere, 2eme ... plus petites valeurs (selon la recopie de la formule).
  • A la recopie LIGNES(E$3:E3) reverra 1, 2 3 etc. permettant de "piocher" les bons n° de ligne via la fonction PETITE.VALEUR.
  • INDEX n'a plus qu'à effectuer son travail.

Formule 2 : Liste des matières

{=SIERREUR(
    INDEX(Pl_Mat;
      PETITE.VALEUR(
         SI(FREQUENCE(
               SI(Pl_Mat<>"";EQUIV(Pl_Mat;Pl_Mat;0));
               LIGNE(Pl_Mat)-1);
             LIGNE(Pl_Mat)-1);
      COLONNES($F2:F2))
        );
"")}

Formule 3 : La moyenne

{=PRODUIT(SI((Pl_Prenom=$E3)*(Pl_Mat=F$2)<>0;$B$2:$B$20))^(1/SOMME((Pl_Prenom=$E3)*(Pl_Mat=F$2)))}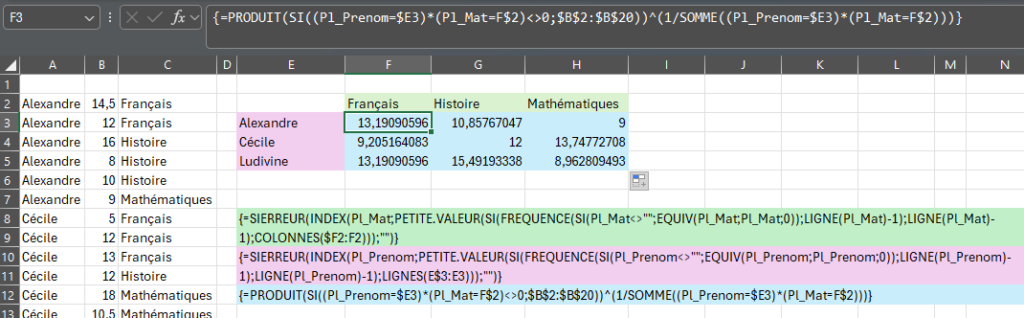

Merci pour votre attention bienveillante.